The most popular method for solving a nonsingular system of linear equations is called Gaussian elimination. It is both simple and effective. The basic idea in elimination is to manipulate the equations of so as to obtain an equivalent set of equations that is easy to solve. is one that has the same solutions.
There are three basic operations used in elimination: (1) multiplying an equation by a nonzero constant, (2) subtracting a multiple of one equation from another, and (3) interchanging rows.
Consider the problem
If we subtract a multiple 
of the first equation from the second,
we get
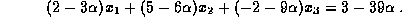
Choosing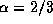 
makes the coefficient of 
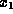zero so that the
unknown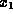 
no longer appears in this equation:
We say that we have ``eliminated'' the unknown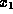 
from the equation.
Similarly, we eliminate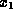 
from equation (1.5) by subtracting
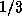times the first equation from it:
The system of equations (1.3)-(1.5) has been reduced to the equivalent system
Now we set aside the first equation and continue the elimination process
with the last two equations in the system (1.6) involving only the
unknowns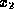 
and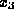 
. Multiply the second equation by 1 and subtract
from the third to produce
a single equation in one unknown. The equations (1.6) have now become the equivalent set of equations
The system (1.8)-(1.10) is easy to solve. From (1.10)
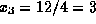. The known value of 
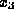is then used in (1.9)
to obtain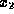 
, i.e.,
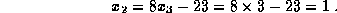
Finally the values for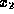 
and 
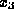are used in (1.8) to
obtain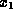 
,
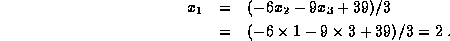
Because this set of equations is equivalent to the original set of
equations, the solution of (1.3)-(1.5) is
, 
, 
.
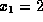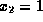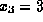